Though I admit to have not given much serious thought to the problem of free will, it certainly is an important one in philosophy. Expressed in simple terms, it asks the following question: "Are our thoughts and actions consequences of decisions made by a larger entity or is it through our own agency?" The presence or the absence of God has always been thought of as a corollary to this answer and my aim in this blog is not to pose an answer but just to complicate the problem further.
Some reasonable people I know, who believe in the non-existence of free will (or are at least inclined towards believing so) state first that our life is governed by the laws of physics, chemistry and biology. No known experiment has, till date, demonstrated the violation of the second law of thermodynamics or achieved speeds faster than that of light. In that regard, I fully agree with them that every known thing in this universe is constrained to obey these laws in its day to day dealings. But does that mean one doesn't have free will?
Let's narrow our speculation to the things on this earth that possess both life and consciousness. A person likes me decides what time to wake up, what cuisine to eat for dinner, what movie to watch and what books to read. I'd like to call the options in each case as degenerate cases under the laws of physics. A recent essay I read about the "finite nature of consciousness" said the following:
Some reasonable people I know, who believe in the non-existence of free will (or are at least inclined towards believing so) state first that our life is governed by the laws of physics, chemistry and biology. No known experiment has, till date, demonstrated the violation of the second law of thermodynamics or achieved speeds faster than that of light. In that regard, I fully agree with them that every known thing in this universe is constrained to obey these laws in its day to day dealings. But does that mean one doesn't have free will?
Let's narrow our speculation to the things on this earth that possess both life and consciousness. A person likes me decides what time to wake up, what cuisine to eat for dinner, what movie to watch and what books to read. I'd like to call the options in each case as degenerate cases under the laws of physics. A recent essay I read about the "finite nature of consciousness" said the following:
Now we know that the brain is a finite physical object, containing roughly 100 million neurons and 100 billion synapses linking the neurons together. But by consciousness being finite, I mean something stronger: that there are only finitely many lives that could possibly be lived; and that therefore free will, if it exists, must at some level be simply the selection of an element from a finite set. The goals of this article are threefold: to show that this proposition is true; to discuss how it affects Penrose's theory of consciousness; and finally to explain why we needn't worry about the finiteness of our minds.
Now this is a slightly disturbing scenario and the reason is this. I don't know much about how our neurons work but if all of them are finite state machines and if that amounts to saying that the total number of states (or configurations) they can take is finite, then this effectively says that the number of thoughts/actions I am capable of is a finite number. The very reason this is disturbing because of the following: As an agnostic, I find it very difficult to believe in the existence of a god who controls my day to day affairs like a puppeteer. I am willing to accommodate a deistic god, in the very least, a creator who rolled the first domino and let the world be. But if I am capable of only finite states, this effectively makes the deistic god capable of specifying a particular trajectory in phase space for every living thing that ever stepped on this earth, one that will be unique (assuming the world will end before as many living beings as the total neuron states step on this earth. The latter is a big big number) but then something that is known before hand. It's like every action that I perform, thinking it has come from my personal choices, has been chronicled in some book in the heavens.
But then an idea from James Gleick's Chaos managed to temporarily placate my fears. I have already mentioned the Lorenz Attractor in one of my earlier posts. Lorenz investigated the following system of deterministic equations in 1963. I downloaded a copy of the original paper and plan to read it as soon as I find some time.
But then an idea from James Gleick's Chaos managed to temporarily placate my fears. I have already mentioned the Lorenz Attractor in one of my earlier posts. Lorenz investigated the following system of deterministic equations in 1963. I downloaded a copy of the original paper and plan to read it as soon as I find some time.
He found two things - the system never settles down to a steady state. In other words it has a trajectory which never repeats itself over time and it is impossible to predict its state unless one numerically follows the equations themselves. At the same time the states of the system are bound - they don't blow up or become infinite. The phase portrait of the system looks like the following (x, y and z plotted on three orthogonal axes with time):
 This elucidates an important fact in case you haven't noticed it yet. Suppose I were a deistic God and I decided that a human X would be governed by the system of three deterministic equations above. The boundedness of the solution would be the equivalent laws of physics that govern terrestrial behaviour (indeed in the case of the equations this seems to be embedded and doesn't call for any extra intervention). But then this deterministic systems yields a solution that is chaotic in a bounded region. It is deterministic but you don't know what it's gonna do next. Another point in this case is that the solution is extremely sensitive to the initial conditions of the differential equations.
This elucidates an important fact in case you haven't noticed it yet. Suppose I were a deistic God and I decided that a human X would be governed by the system of three deterministic equations above. The boundedness of the solution would be the equivalent laws of physics that govern terrestrial behaviour (indeed in the case of the equations this seems to be embedded and doesn't call for any extra intervention). But then this deterministic systems yields a solution that is chaotic in a bounded region. It is deterministic but you don't know what it's gonna do next. Another point in this case is that the solution is extremely sensitive to the initial conditions of the differential equations.My argument is hardly complete and I do not intend to reach a denouement here. All I wanted to share was that it is possible to reconcile determinism with free will in a way. Whatever the system is going to do exists as hidden information in the three simple differential equations. But it is impossible for a person to deduce that unless the system itself is simulated. And then again, knowing the system at a point in time is not going to help one realize what it's gonna be doing ten milliseconds, hours or years from then.
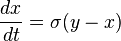



1 comment:
I should digg your article so more folks are able to see it, really useful, I had a hard time finding the results searching on the web, thanks.
- Thomas
Post a Comment